De kortste verbinding.
Het probleem:
Er zijn drie plaatsen, A, B en C, die met elkaar verbonden moeten worden. Hoe moet dat gebeuren om de totale lengte van alle verbindingslijnen zo klein mogelijk te maken?

De oplossing:
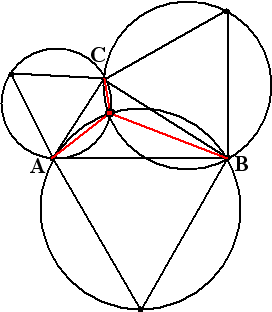
Teken driehoek ABC en op elke zijde daarvan een gelijkzijdige driehoek.
Construeer van al deze driehoeken de omgeschreven cirkel.
Het snijpunt van deze drie omgeschreven cirkels is het punt van Fermat (of Steinerpunt) van de driehoek, en je vindt de kortste verbinding door de hoeken met dit punt te verbinden.  De hoeken tussen de verbindingslijnen zijn altijd 120º.

't Kan ook fysisch: hang gelijke gewichten aan touwtjes die door de hoekpunten van de driehoek gaan. Waar de knoop terechtkomt ligt het gezochte punt.
De volgende vraag is natuurlijk hoe het gaat bij 4 punten. In dat geval teken je de vierhoek ABCD, en construeer je op twee tegenover elkaar liggende zijden ervan een gelijkzijdige driehoek. Verbind de punten van die driehoeken die niet op de vierhoek liggen met elkaar. Dat geeft twee snijpunten met de omgeschreven cirkels van die driehoeken. Dat zijn de twee gezochte punten voor het netwerk. Zo'n netwerk heet wel een Steiner-netwerk. De hoeken zijn weer 120º trouwens....