| Twee
belangrijke stellingen. |
|
|
De regel van Euler voor kaarten in
een vlak leverde ons op
Daarbij is L = aantal landen, K = aantal knooppunten en G
= aantal grenzen. Het buitengebied van de kaart geldt ook als
een land, dus elke kaart is oneindig groot.
Met deze regel gaan we twee belangrijke stellingen afleiden die
eigenlijk in elke oplossing voor het vierkleurenprobleem terug
te vinden zijn. |
|
|
De eerste stelling is:
|
| Elke kaart heeft minstens
één land met vijf of minder buren. |
|
|
Het bewijs gaat als volgt.
| 1. |
Bij elk knooppunt komen
minstens drie grenzen samen (knooppunten met twee
grenzen bestaan uit een lijn met een stip erin en die
kunnen we net zo goed weglaten).
Dus er zijn 3K grenzen, maar omdat dan elke grens dubbel
is geteld levert dat 3/2K
grenzen.
Ofwel: G ³ 3/2K
Þ K
£ 2/3G |
| 2. |
Stel dat er geen land met
vijf of minder buren is, dan heeft elk land dus 6 of
meer buren.
Met elke buur heeft zo'n land een grens, dus dan zijn er
minstens 6L grenzen.
Omdat weer alle grenzen dubbel zijn geteld geldt G
³ 6/2L
Þ G ³
3L ofwel L £
1/3G |
| 3. |
Euler's formule geeft
dan L + K - G = 2
Invullen levert 1/3G
+ 2/3G - G £
2 en dat geeft 0 £
2
Dat is natuurlijk flauwekul, dus kan aanname 2. niet
waar zijn. |
Deze stelling zullen we voortaan de "vijfburenstelling"
noemen. |
|
|
De tweede stelling heet de "telstelling".
Stel Li het aantal landen met i grenzen
is.
Dan is L = L2 + L3
+ L4... (een land met één grens bestaat
misschien wel, maar kunnen we wat kleuren betreft net zo goed
weglaten)
Voor het aantal grenzen G geldt dan 2L2 +
3L3 + 4L4 + .... = 2G (de factor 2
omdat elke grens weer dubbel is geteld)
Dus G = L2 + 11/2L3
+ 2L4 + ...
Omdat bij elk knooppunt 3 grenzen bij elkaar komen (zoals we in
een eerdere vereenvoudiging al zagen), geldt:
2L2 + 3L3 + 4L4 = 3K want
beide kanten geven het totaal aantal grenzen aan.
daaruit volgt: K = 2/3L2
+ L3 + 4/3L4
+ .....
Je raadt het al: nu gewoon alles invullen in de formule
van Euler:
L + K - G = 2 Þ (L2
+ L3 + L4...) + (2/3L2
+ L3 + 4/3L4
+ .....) - (L2 + 11/2L3
+ 2L4 + ...) = 2
herrangschikken en met 6 vermenigvuldigen:
|
| 4L2 + 3L3
+ 2L4 + L5 - L7
- 2L8 - 3L9 - ... = 12 |
|
|
|
En dat is de telstelling.
Als kleine toepassing zie je bijvoorbeeld al dat een kaart met
alleen vijfhoeken of hoger minstens 12 vijfhoeken moet hebben.
(als L2 = L3 = L4 = 0 moet L5
minstens 12 zijn). Dat heeft bijvoorbeeld weer als gevolg dat
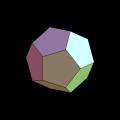
een veelvlak met alleen vijfhoeken en zeshoeken precies 12
vijfhoeken zal hebben. Dat is inderdaad zo, kijk maar naar het
regelmatige twaalfvlak en de beroemde Buckeyball: beiden bestaan
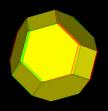
uit exact 12 vijfhoeken. En het afgeknotte achtvlak, dat bestaat
uit vierkant en zeshoeken zal natuurlijk precies 6 vierkant
moeten hebben (2L4 = 12). Dat zie je in de derde
figuur hieronder. |
|
|
 |
|
 |
|
 |
| twaalfvlak |
|
voetbal |
|
afgeknot achtvlak |
|
|
|
| 't Is mooi dat dat tenminste allemaal klopt... |
|