De Regel van Euler.
We beginnen met de beroemde regel van Euler. Hij onderzocht veelvlakken (een veelvlak is een ruimtelijke figuur die omsloten wordt door allemaal platte vlakken. Noem H het aantal hoekpunten, R het aantal ribben en V het aantal vlakken.

Dan zegt de regel van Euler:
V + H = R + 2
Hier staat dat uitgewerkt voor de vijf regelmatige (Platonische) veelvlakken, maar het geldt ook voor niet-regelmatige veelvlakken.
Euler zelf gaf een bewijs van zijn regel door steeds viervlak-vormen van een willekeurig veelvlak af te halen (waarbij zijn regel geldig bleef) en uiteindelijk elk veelvlak te reduceren tot een viervlak. Zijn bewijs (uit 1751) was echter niet helemaal kloppend.
In 1794 bewees Legendre de regel voor het eerst écht.

Nou zagen we al eerder dat het tekenen van een kaart op een bol hetzelfde is als het tekenen op een plat vlak. Daarom geldt de regel van Euler dus óók voor vlakke kaarten, als we nemen:  V = aantal landen,  H = aantal knooppunten en  R = aantal grenzen. Vanaf nu geldt dus voor al onze kaarten:

L + K = G + 2

opmerking: om de bol helemaal op het platte vlak te projecteren is het wel nodig dat we het buitengebied van een kaart óók als een land zien, immers de noordpool komt terecht op "oneindig". Het bewijs van de regel van Euler kan dan door van een gegeven kaart langzaamaan één voor één de grenzen weg te laten (en losse punten ook) en te controleren dat daarbij steeds de regel geldig blijft.
Bij het weglaten van een grens zijn er 2 mogelijkheden:

1. De grens scheidt twee landen
Bij het weglaten wordt dan  G één minder en ook L (want twee landen worden één.
Dus blijft gelden L + K = G + 2
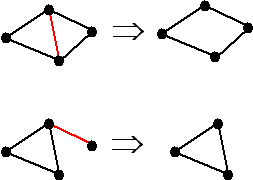2. De grens hangt los.
Bij het weglaten wordt dan G één lager, en K óók (het losse punt verdwijnt)
Dus blijft gelden  L + K = G + 2

Als we steeds eerst alle loshangende grenzen doen dan zijn dit de enige twee mogelijkheden.
Zo eindigen we altijd met één grens met twee punten en één vlak. Daarvoor geldt  1 + 2 = 1 + 2 dus de regel klopt.