| De
denkfout van Möbius. |
|
|
Soms wordt beweerd
dat het vierkleurenprobleem al dateert van rond 1840 toen de
Duitse wiskundige Ferdinand Möbius een lezing hield waarin hij
het "Probleem van de vijf prinsen" noemde. Dat
probleem luidt als volgt:
|
Er leefde eens in India een
koning die vijf zonen had.
De koning zei dat na zijn dood de zonen het
koninkrijk onder elkaar mochten verdelen, maar
alleen zó dat het gebied van elke zoon zou
grenzen aan dat van alle andere zonen.
Hoe moesten ze dat aanpakken? |
|
|
Hier wordt een voorbeeld gevraagd wordt van een
kaart waarvoor vijf kleuren nodig zijn.
Dat dat onmogelijk is, is eenvoudig te zien.
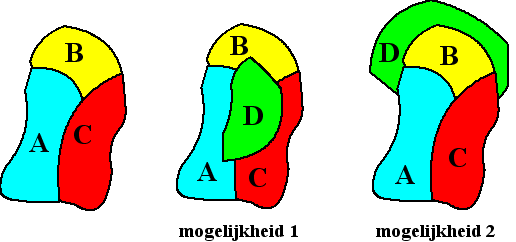
Stel dat de gebieden van de eerste drie zonen A, B en C zijn.
Dan zijn er voor het gebied van zoon D twee mogelijkheden: Het
ligt helemaal binnen de oppervlakte ABC of helemaal erbuiten: |
|
|
 |
|
|
Maar nu is er in
beide gevallen voor het laatste gebied geen mogelijkheid meer.
Misschien is het nog duidelijker te zien als je het probleem in
een ander jasje hijst: het probleem van de
vijf paleizen:
|
| De koning eist verder nog dat
elk van zijn zonen een paleis op zijn eigen
gebied bouwt, en dat alle vijf de paleizen met
elkaar verbonden zullen worden door een weg
zonder dat al die wegen elkaar mogen kruisen. |
|
|
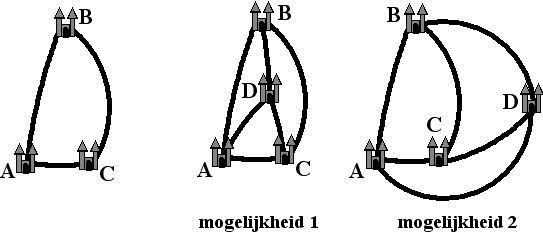
Stel weer dat de eerste drie paleizen A,B en C heten, dan
zijn die dus als een driehoek verbonden. Paleis D kan óf binnen
deze driehoek liggen óf erbuiten. Maar in beide gevallen is
paleis E niet te bouwen (in het eerste geval is D niet te
bereiken, in het tweede geval één van de andere drie niet; in
het voorbeeld hieronder C). |
|
|
 |
|
|
|
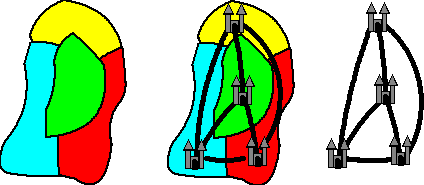
| Dat deze twee
problemen exact gelijk zijn zie je als je de figuren over elkaar
heen legt. Lees als paleis "land" en als weg
"grens" en klaar! Kijk maar hiernaast.
We hebben nu wel laten zien dat het verdelen van het land
onder de vijf prinsen onmogelijk is, maar toch is daarmee het
vierkleurenprobleem niet opgelost! Wie dat denkt maakt een
denkfout!
HOE ZIT DAT? |
|
|
Het ziet hem in de
logica!
Stel P = "er bestaat een kaart met 5 elkaar rakende
gebieden" en Q = "elke kaart kan met 4
kleuren gekleurd worden"
De conclusie die we uit het bovenstaande kunnen trekken is:
|
BEWERING 1
"ALS er geen kaart met vijf elkaar rakende
gebieden bestaat DAN kan elke kaart met 4
kleuren worden gekleurd"
ofwel: ¬P Þ Q |
|
|
¬ betekent "niet".
Terwijl het vierkleurenprobleem stelt:
|
BEWERING 2
"ALS er een kaart met vijf elkaar rakende
gebieden bestaat DAN kan niet elke kaart met 4
kleuren worden gekleurd".
dat is logisch genoteerd P Þ
¬Q |
|
|
Dat mogen we omdraaien en "niet" ervoor
zetten.
Dan vinden we Q Þ ¬P
:
|
BEWERING 3
"ALS elke kaart met 4 kleuren kan worden
gekleurd, DAN bestaat er geen kaart met vijf
elkaar rakende gebieden" |
|
|
En dat is een andere bewering dan bewering 1
hierboven. P Þ Q is niet
gelijk aan Q Þ P.
|
|
|