| De gemarkeerde liniaal. |
|
|
Het is haast niet te geloven maar dit simpele liniaaltje, met slechts twee streepjes erop, kan een hoek in drieën
delen én de kubus verdubbelen.
Archimedes ontdekte dat al. |
 |
| Dat gaat als volgt in z'n werk:
1. Hoek in drieën
|
|
 |
|
|
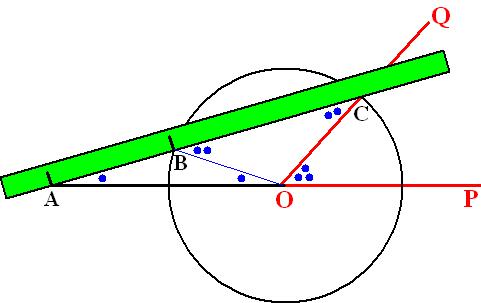
Neem hoek POQ met hoekpunt O.
Teken een cirkel om O met straal AB (die van het liniaaltje)
Verleng been OP aan de andere kant van O.
Leg het liniaaltje nu neer bij het snijpunt van de cirkel met het andere
been van de hoek: punt C.
Draai en schuif het vervolgens zó dat A op het verlengde been komt te
liggen en B op de cirkel.
Dan is hoek OAB 1/3 van POQ.
Waarom?
OB = BA dus beide hoeken met de enkele blauwe stip zijn gelijk.
Dan is ∠ABO gelijk aan 180º - 2 blauwe
stippen. Dus is ∠OBC weer gelijk aan twee blauwe
stippen.
OB = OC dus ook ∠OCB is twee blauwe stippen.
Dan is ∠COB = 180º - 4 blauwe stippen
Dus zijn ∠AOB en ∠POC
samen 4 blauwe stippen.
Maar ∠AOB is één blauwe stip, dus ∠POC
is drie blauwe stippen. |
|
|
| 2. Kubus
Verdubbelen. |
|
|
|
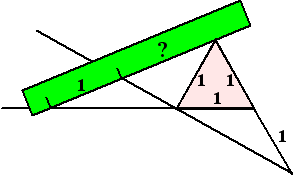
Neem aan dat de streepjes 1 eenheid uit
elkaar staan.
Teken dan eerst een gelijkzijdige driehoek met zijden 1.
Verleng één van de zijden met 1, trek een lijn van het zo gekregen
eindpunt door het derde hoekpunt van de driehoek.
Leg het liniaaltje neer als hiernaast en het vraagteken is precies 3√2.
|
 |
|
|