| De
Kwadratrix van Hippias |
|
|
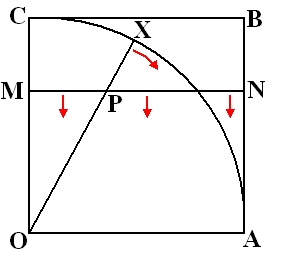
Kijk maar eens naar de figuur hiernaast.
AC is een cirkelboog, OABC is een vierkant.
We laten nu tegelijkertijd een punt X met constante hoeksnelheid draaien
van C naar A, en tegelijkertijd laten we een lijnstuk MN met
constante snelheid zakken van CB naar OA.
Als X dan 1/3 deel van
zijn baan heeft afgelegd, dan heeft MN dat ook, dus dan bevindt MN
zich op afstand 1/3 van CO vanaf
C.
Opdat moment is ∠XOC precies 1/3
van de rechte hoek.
En dit verhaal geldt niet alleen voor een rechte hoek, maar
voor elke hoek AOC. Op deze manier is het in drieŽn delen van een
hoek teruggebracht tot het in drieŽn delen van een lijnstuk (OC
in dit geval).
|
 |
|
|
| Waar liggen de punten P? |
|
|
|
Neem OA = OC = 1, noem ∠XOA
=
φ en noem P(x,y)
Dan geldt: tan
φ = x/y
⇒ y = x ē tan
φ
.....(1)
Maar vanwege de constante draai- en zaksnelheden moet ook
gelden:
|
Dat wil zeggen dat y/φ
= 2/π
⇒
φ = y ē
π/2
Invullen in vergelijking (1) geeft: y
= x ē tan(0,5πy)
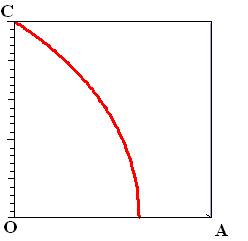
Dat is een impliciete vergelijking die we met de computer
makkelijk kunnen plotten (bijvoorbeeld met WINPLOT dat hier
gratis is te downloaden). De kromme ziet eruit als
hiernaast. Het is de Kwadratrix van Hippias.
|
 |
| Hoe delen we nu een hoek in
drieŽn? |
|
|
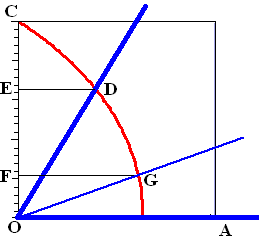
Teken de figuur hierboven op doorzichtig papier
(een sheet bijvoorbeeld)
Leg OA langs ťťn been van de hoek, en laat het andere been
ergens tussen OA en OC liggen.
D is het snijpunt van het tweede been met de kwadratrix.
Trek een lijn van D evenwijdig aan OA naar OC toe, en noem dat
punt E
Gebruik de schaalverdeling van OC om OE in drieŽn te delen; dat
geeft punt F.
Trek een lijn van F evenwijdig aan OA weer terug naar de
kwadratrix; dat geeft punt G
Nu is hoek GOA 1/3
deel van de hele hoek. |
 |