| In het algemeen kun je een
cisso´de construeren voor elke twee krommen en een vast punt.
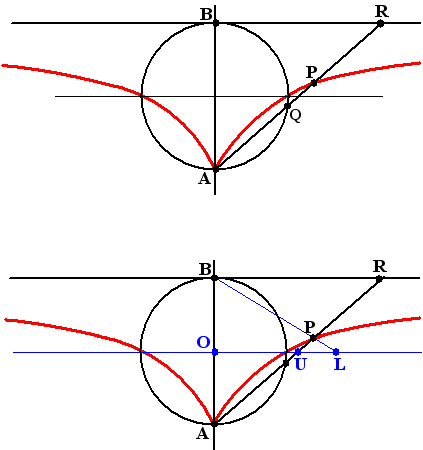
De cisso´de van Diocles gebruikt een cirkel, een raaklijn
eraan, en het punt tegenover het raakpunt.
De constructie is als volgt:
Trek een lijn door A die de cirkel in Q snijdt en de raaklijn in
R.
Kies punt P op deze lijn zodat AP = QR.
De verzameling van alle punten P is dan de cisso´de van Diocles.
Zo verdubbel je de kubus:
Trek een lijn door het middelpunt van de cirkel evenwijdig
aan de raaklijn.
Snij BP met deze lijn; dat geeft punt L.
U is het snijpunt van AR met OL.
Als de straal van de cirkel 1 is, dan is nu OU3 =
OL
Dus als OL = 2, dan is OU = 3√2.
Om 3√2
te construeren werken we dus andersom: neem OL = 2, trek BL, en
P is het snijpunt met de cisso´de, trek AP, en U is het
snijpunt met OL.
|
 |