© h.hofstede (h.hofstede@hogeland.nl)

   
Inductie
Proof By Induction:
1.  Obtain a large power transformer
2.  Find someone who does not believe your theorem
3.  Get him to hold the terminals of your generator
4.  Apply 25000 Volts AC to the generator
5.  Repeat step 4 until he agrees with the theorem

Inductie is de meest aparte en ook meest misbruikte bewijsmethode. Stel dat we een bepaalde eigenschap voor alle gehele getallen vanaf  n  moeten bewijzen. Dan gaat een inductieredenering zo:

stap 1: laat zien dat de eigenschap voor n waar is
stap 2:  laat zien dat, als de eigenschap voor een getal p geldt, dat hij dan ook geldt voor p + 1.

Als de eigenschap voor n geldt, dan geldt hij (met stap 2) ook voor n + 1, maar daarna (weer volgens stap 2) ook voor n + 2, enzovoorts. Dus geldt de stelling voor elke waarde vanaf n.

Het bewijs van de stelling van Gauss hierboven zou inductief als volgt gaan:

stap 1.   De stelling geldt voor n = 1  want  1 = ½ • 1 • 2

stap 2.
 

 

 

 

 

 

 Stel dat  1 + 2 + 3 + ... + p =  ½ • p • (p + 1)
 Te bewijzen dat dan ook geldt:
 1 + 2 + 3 + ... + p + (p + 1) =  ½ • (p + 1) • {(p +1) + 1)}
 En dat bewijs gaat als volgt: 
1 + 2 + 3 + ... + p + (p + 1)
= 1/2 • p • (p + 1) + (p + 1) volgens stap 1
= 1/2 • p • (p + 1) + 1/2•2•(p + 1) want 1/2 • 2 = 1
= 1/2 • (p + 1) • (p + 2) 
= 1/2 • (p + 1) • {(p + 1) + 1} 

Kijk uit dat je de volgende stap wel echt bewijst. Dat je je aardig kunt vergissen blijkt misschien wel uit de volgende serie. We gaan een cirkel verdelen in segmenten door een aantal punten op de omtrek met elkaar te verbinden. Als we steeds een punt toevoegen groeit het aantal segmenten.
Hieronder staat het maximaal aantal segmenten.

Je denkt uiteraard "bewezen" te hebben dat de laatste cirkel wel 32 segmenten zal bevatten. 

Maar is dat wel zo.....

open          oefeningen inductie (11)        sluit

Tweestaps-inductie ("leap-frog induction")

Er zijn ook inductiebewijzen die niet van p naar p + 1 gaan,  maar van p naar p + 2. 
Hier is er zo eentje:

Voor elke n > 3 bestaat er een n-hoek met niet allemaal gelijke zijden, 
zodat som van de afstanden van een punt erbinnen naar alle zijden constant is. 

(Voor n = 3  klopt dit niet, want de enige driehoek waarvoor de som van de afstanden naar de drie zijden constant is, is de gelijkzijdige driehoek.)
Voor n = 4 klopt de stelling wél: neem maar een willekeurige rechthoek!

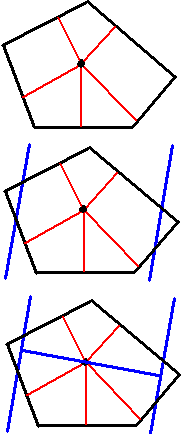
De inductiestap:

Stel dat de stelling voor een bepaalde n-hoek geldt (zie hiernaast). Dan kiezen we een richting die niet evenwijdig is aan een zijde, en trekken in deze richting twee evenwijdige (blauwe) lijnen. Daarmee snijden we twee hoeken van de n-hoek af.

Dat geeft een n + 2-hoek. Het afsnijden kunnen we altijd wel zó regelen dat de twee nieuwe zijden niet even lang zijn.

De som van de afstanden van een punt van deze nieuwe figuur naar alle zijden is constant. Immers de som van de afstanden tot de "oude" zijden van de n-hoek is constant (de rode lijnen), en daar zijn nu twee nieuwe afstanden bijgekomen (de blauwe lijnen). Maar die zijn samen altijd precies gelijk aan de afstand tussen de twee evenwijdige lijnen. Dus de totale afstand blijft constant.
Daarmee is de inductiestap voltooid.

Maar ja, deze inductie gaat van n naar n + 2, dus moeten we als eerste stap niet alleen n = 4 (de rechthoek) controleren, maar óók n = 5.
Gelukkig is die makkelijk te vinden: begin maar met een gelijkzijdige driehoek en snij daar volgens de methode hierboven met twee evenwijdige lijnen twee hoeken af. Dat geeft een vijfhoek waarvoor de eigenschap geldt.

Meer tweestapsinductie:


Polya's Paradox

Er is nog iets vreemds met sommige inductiebewijzen aan de hand; soms is het niet mogelijk een bepaalde bewering met inductie te bewijzen, maar kun je wél een nog veel sterkere bewering bewijzen!  Neem het volgende voorbeeld. 
Stel dat we willen bewijzen:

Als we dat met inductie proberen zouden we aannemen dat de stelling geldt voor  n en dan proberen te bewijzen voor n + 1. Dat geeft dan:

Waarbij we het laatste kleiner-dan teken nog moeten bewijzen. Maar dat lukt niet!
Als we alles kwadrateren (mag want het is toch allemaal positief), en daarna haakjes wegwerken en alles naar één kant brengen, dan blijft over  3n + 3 < 0.
En dat is duidelijk niet waar.

Maar zie wat er gebeurt als we onze voorwaarde nog strenger maken:

Nu is het opeens wél met inductie te bewijzen. Precies dezelfde procedure als hierboven levert nu op  
8n2 + 17n + 8 > 0  En dat is voor n > 0 inderdaad altijd het geval, zoals je wel aan de parabool hiernaast kunt zien.

Nu hebben we dus een strenger geval bewezen, dus ook het oorspronkelijke geval. Maar het eerste lukte niet met inductie en dit tweede wél.

Vreemd hè?

Hier zijn er nog een paar:

 

© h.hofstede (h.hofstede@hogeland.nl)